Waves Wikipedia

Waves Wikipedia.                GeniusJarvis.blogspot.com.                                             

• Home
• Random
• Nearby

• Log in

• Settings

• About Wikipedia
 
• Disclaimers

Open main menu

Wave

• Read in another language
• Watch this page
• Edit

This article is about waves in the scientific sense. For waves on seas and lakes, see Wind wave. For other uses, see Wave (disambiguation).

Surface waves in water showing water ripples

Different types of wave with varying rectifications

In physics, mathematics, and related fields, a wave is a disturbance (change from equilibrium) of one or more fields such that the field values oscillate repeatedly about a stable equilibrium (resting) value. If the relative amplitude of oscillation at different points in the field remains constant, the wave is said to be a standing wave. If the relative amplitude at different points in the field changes, the wave is said to be a traveling wave. Waves can only exist in fields when there is a force that tends to restore the field to equilibrium.

The types of waves most commonly studied in physics are mechanical and electromagnetic. In a mechanical wave, stress and strain fields oscillate about a mechanical equilibrium. A traveling mechanical wave is a local deformation (strain) in some physical medium that propagates from particle to particle by creating local stresses that cause strain in neighboring particles too. For example, sound waves in air are variations of the local pressure that propagate by collisions between gas molecules. Other examples of mechanical waves are seismic waves, gravity waves, vortices, and shock waves. In an electromagnetic wave the electric and magnetic fields oscillate. A traveling electromagnetic wave (light) consists of a combination of variable electric and magnetic fields, that propagates through space according to Maxwell's equations. Electromagnetic waves can travel through transparent dielectric media or through a vacuum; examples include radio waves, infrared radiation, visible light, ultraviolet radiation, X-rays and gamma rays.

Other types of waves include gravitational waves, which are disturbances in a gravitational field that propagate according to general relativity; heat diffusion waves; plasma waves, that combine mechanical deformations and electromagnetic fields; reaction-diffusion waves, such as in the Belousov–Zhabotinsky reaction; and many more.

Mechanical and electromagnetic waves transfer energy,^[1], momentum, and information, but they do not transfer particles in the medium. In mathematics and electronics waves are studied as signals.^[2] On the other hand, some waves do not appear to move at all, like standing waves (which are fundamental to music) and hydraulic jumps. Some, like the probability waves of quantum mechanics, may be completely static.

A physical wave is almost always confined to some finite region of space, called its domain. For example, the seismic waves generated by earthquakes are significant only in the interior and surface of the planet, so they can be ignored outside it. However, waves with infinite domain, that extend over the whole space, are commonly studied in mathematics, and are very valuable tools for understanding physical waves in finite domains.

A plane wave seems to travel in a definite direction, and has constant value over any plane perpendicular to that direction. Mathematically, the simplest waves are the sinusoidal ones in which each point in the field experiences simple harmonic motion. Complicated waves can often be described as the sum of many sinusoidal plane waves. A plane wave can be a transverse, if its effect at each point is described by a vector that is perpendicular to the direction of propagation or energy transfer; or longitudinal, if the describing vectors are parallel to the direction of energy propagation. While mechanical waves can be both transverse and longitudinal, electromagnetic waves are transverse in free space.

Mathematical DescriptionEdit

Single wavesEdit

A wave can be described just like a field, namely as a function ${\displaystyle F(x,t)}$ where ${\displaystyle x}$ is a position and ${\displaystyle t}$ is a time.

The value of ${\displaystyle x}$ is a point of space, specifically in the region where the wave is defined. In mathematical terms, it is usually a vector in the Cartesian three-dimensional space ${\displaystyle \mathbb {R} ^{3}}$. However, in many cases one can ignore one dimension, and let ${\displaystyle x}$ be a point of the Cartesian plane ${\displaystyle \mathbb {R} ^{2}}$. This is the case, for example, when studying vibrations of a drum skin. One may even restrict ${\displaystyle x}$ to a point of the Cartesian line ${\displaystyle \mathbb {R} }$ — that is, the set of real numbers. This is the case, for example, when studying vibrations in a violin string or recorder. The time ${\displaystyle t}$, on the other hand, is always assumed to be a scalar; that is, a real number.

The value of ${\displaystyle F(x,t)}$ can be any physical quantity of interest assigned to the point ${\displaystyle x}$ that may vary with time. For example, if ${\displaystyle F}$ represents the vibrations inside an elastic solid, the value of ${\displaystyle F(x,t)}$ is usually a vector that gives the current displacement from ${\displaystyle x}$ of the material particles that would be at the point ${\displaystyle x}$ in the absence of vibration. For an electromagnetic wave, the value of ${\displaystyle F}$ can be the electric field vector ${\displaystyle E}$, or the magnetic field vector ${\displaystyle H}$, or any related quantity, such as the Poynting vector ${\displaystyle E\times H}$. In fluid dynamics, the value of ${\displaystyle F(x,t)}$ could be the velocity vector of the fluid at the point ${\displaystyle x}$, or any scalar property like pressure, temperature, or density. In a chemical reaction, ${\displaystyle F(x,t)}$ could be the concentration of some substance in the neighborhood of point ${\displaystyle x}$ of the reaction medium.

For any dimension ${\displaystyle d}$ (1, 2, or 3), the wave's domain is then a subset ${\displaystyle D}$ of ${\displaystyle \mathbb {R} ^{d}}$, such that the function value ${\displaystyle F(x,t)}$ is defined for any point ${\displaystyle x}$ in ${\displaystyle D}$. For example, when describing the motion of a drum skin, one can consider ${\displaystyle D}$ to be a disk (circle) on the plane ${\displaystyle \mathbb {R} ^{2}}$ with center at the origin ${\displaystyle (0,0)}$, and let ${\displaystyle F(x,t)}$ be the vertical displacement of the skin at the point ${\displaystyle x}$ of ${\displaystyle D}$ and at time ${\displaystyle t}$.

Wave familiesEdit

Sometimes one is interested in a single specific wave, like how the Earth vibrated after the 1929 Murchison earthquake. More often, however, one needs to understand large set of possible waves; like all the ways that a drum skin can vibrate after being struck once with a drum stick, or all the possible radar echos one could get from an airplane that may be approaching an airport.

In some of those situations, one may describe such a family of waves by a function ${\displaystyle F(A,B,\ldots ;x,t)}$ that depends on certain parameters ${\displaystyle A,B,\ldots }$, besides ${\displaystyle x}$ and ${\displaystyle t}$. Then one can obtain different waves — that is, different functions of ${\displaystyle x}$ and ${\displaystyle t}$ — by choosing different values for those parameters.

Sound pressure wave in a half-open pipe playing the 7th harmonic of the fundamental (n = 4).

For example, the sound pressure inside a recorder that is playing a "pure" note is typically a standing wave, that can be written as

${\displaystyle F(A,L,n,c;x,t)=A\,(\cos 2\pi x{\frac {2n-1}{4L}})(\cos 2\pi ct{\frac {2n-1}{4L}})}$

The parameter ${\displaystyle A}$ defines the amplitude of the wave (that is, the maximum sound pressure in the bore, which is related to the loudness of the note); ${\displaystyle c}$ is the speed of sound; ${\displaystyle L}$ is the length of the bore; and ${\displaystyle n}$ is a positive integer (1,2,3,...) that specifies the number of nodes in the standing wave. (The position ${\displaystyle x}$ should be masured from the mouthpiece, and the time ${\displaystyle t}$ from any moment at which the pressure at the mouthpiece is maximum. The quantity ${\displaystyle \lambda =4L/(2n-1)}$ is the wavelength of the emitted note, and ${\displaystyle f=c/\lambda }$ is its frequency.) Many general properties of these waves can be inferred from this general equation, without choosing specific values for the parameters.

As another example, it may be that the vibrations of a drum skin after a single strike depend only on the distance ${\displaystyle r}$ from the center of the skin to the strike point, and on the strength ${\displaystyle s}$ of the strike. Then the vibration for all possible strikes can be described by a function ${\displaystyle F(r,s;x,t)}$.

Sometimes the family of waves of interest has infinitely many parameters. For example, one may want to describe what happens to the temperature in a metal bar when it is initially heated at various temperatures at different points along its length, and then allowed to cool by itself in vacuum. In that case, instead of a scalar or vector, the parameter would have to be a function ${\displaystyle h}$ such that ${\displaystyle h(x)}$ is the initial temperature at each point ${\displaystyle x}$ of the bar. Then the temperatures at later times can be expressed by a function ${\displaystyle F}$ that depends on the function ${\displaystyle h}$ (that is, a functional operator), so that the temperature at a later time is ${\displaystyle F(h;x,t)}$

Differential wave equationsEdit

Another way to describe and study a family of waves is to give a mathematical equation that, instead of explicitly giving the value of ${\displaystyle F(x,t)}$, only constrains how those values can change with time. Then the family of waves in question consists of all functions ${\displaystyle F}$ that satisfy those constraints — that is, all solutions of the equation.

This approach is extremely important in physics, because the constraints usually are a consequence of the physical processes that cause the wave to evolve. For example, if ${\displaystyle F(x,t)}$ is the temperature inside a block of some homogeneous and isotropic solid material, its evolution is constrained by the partial differential equation

${\displaystyle {\frac {\partial F}{\partial t}}(x,t)=\alpha \left({\frac {\partial ^{2}F}{\partial x_{1}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{2}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{3}^{2}}}(x,t)\right)+\beta Q(x,t)}$

where ${\displaystyle Q(p,f)}$ is the heat that is being generated per unit of volume and time in the neighborhood of ${\displaystyle x}$ at time ${\displaystyle t}$ (for example, by chemical reactions happening there); ${\displaystyle x_{1},x_{2},x_{3}}$ are the Cartesian coordinates of the point ${\displaystyle x}$; ${\displaystyle \partial F/\partial t}$ is the (first) derivative of ${\displaystyle F}$ with respect to ${\displaystyle t}$; and ${\displaystyle \partial ^{2}F/\partial x_{i}^{2}}$ is the second derivative of ${\displaystyle F}$ relative to ${\displaystyle x_{i}}$. (The simbol "${\displaystyle \partial }$" is meant to signify that, in the derivative with respect to some variable, all other variables must be considered fixed.)

This equation can be derived from the laws of physics that govern the diffusion of heat in solid media. For that reason, it is called the heat equation in mathematics, even though it applies to many other physical quantities besides temperatures.

For another example, we can describe all possible sounds echoing within a container of gas by a function ${\displaystyle F(x,t)}$ that gives the pressure at a point ${\displaystyle x}$ and time ${\displaystyle t}$ within that container. If the gas was initially at uniform temperature and composition, the evolution of ${\displaystyle F}$ is constrained by the formula

${\displaystyle {\frac {\partial ^{2}F}{\partial t^{2}}}(x,t)=\alpha \left({\frac {\partial ^{2}F}{\partial x_{1}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{2}^{2}}}(x,t)+{\frac {\partial ^{2}F}{\partial x_{3}^{2}}}(x,t)\right)+\beta P(x,t)}$

Here ${\displaystyle P(x,t)}$ is some extra compression force that is being applied to the gas near ${\displaystyle x}$ by some external process, such as a loudspeaker or piston right next to ${\displaystyle p}$.

This same differential equation describes the behavior of mechanical vibrations and electromagnetic fields in a homogeneous isotropic non-conducting solid. Note that this equation differs from that of heat flow only in that the left-hand side is ${\displaystyle \partial ^{2}F/\partial t^{2}}$, the second derivative of with respect to time, rather than the first derivative ${\displaystyle \partial F/\partial t}$. Yet this small change makes a huge difference on the set of solutions ${\displaystyle F}$. This differential equation is called "the" wave equation in mathematics, even though it describes only one very special kind of waves.

Wave in elastic mediumEdit

Main articles: Wave equation and D'Alembert's formula

Consider a traveling transverse wave (which may be a pulse) on a string (the medium). Consider the string to have a single spatial dimension. Consider this wave as traveling

Wavelength λ, can be measured between any two corresponding points on a waveform

Animation of two waves, the green wave moves to the right while blue wave moves to the left, the net red wave amplitude at each point is the sum of the amplitudes of the individual waves. Note that f(x,t) + g(x,t) = u(x,t)

• in the ${\displaystyle x}$ direction in space. For example, let the positive ${\displaystyle x}$ direction be to the right, and the negative ${\displaystyle x}$ direction be to the left.
• with constant amplitude ${\displaystyle u}$
• with constant velocity ${\displaystyle v}$, where ${\displaystyle v}$ is
  • independent of wavelength (no dispersion)
  • independent of amplitude (linear media, not nonlinear).^[3][4]
• with constant waveform, or shape

This wave can then be described by the two-dimensional functions

${\displaystyle u(x,t)=F(x-v\ t)}$ (waveform ${\displaystyle F}$ traveling to the right)

${\displaystyle u(x,t)=G(x+v\ t)}$ (waveform ${\displaystyle G}$ traveling to the left)

or, more generally, by d'Alembert's formula:^[5]

${\displaystyle u(x,t)=F(x-vt)+G(x+vt).\,}$

representing two component waveforms ${\displaystyle F}$ and ${\displaystyle G}$ traveling through the medium in opposite directions. A generalized representation of this wave can be obtained^[6] as the partial differential equation

${\displaystyle {\frac {1}{v^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}={\frac {\partial ^{2}u}{\partial x^{2}}}.\,}$

General solutions are based upon Duhamel's principle.^[7]

Wave formsEdit

Main article: Waveform

Sine, square, triangle and sawtooth waveforms.

The form or shape of F in d'Alembert's formula involves the argument x − vt. Constant values of this argument correspond to constant values of F, and these constant values occur if x increases at the same rate that vt increases. That is, the wave shaped like the function F will move in the positive x-direction at velocity v (and G will propagate at the same speed in the negative x-direction).^[8]

In the case of a periodic function F with period λ, that is, F(x + λ − vt) = F(x − vt), the periodicity of F in space means that a snapshot of the wave at a given time t finds the wave varying periodically in space with period λ (the wavelength of the wave). In a similar fashion, this periodicity of F implies a periodicity in time as well: F(x − v(t + T)) = F(x − vt) provided vT = λ, so an observation of the wave at a fixed location x finds the wave undulating periodically in time with period T = λ/v.^[9]

Amplitude and modulationEdit

Amplitude modulation can be achieved through f(x,t) = 1.00*sin(2*pi/0.10*(x-1.00*t)) and g(x,t) = 1.00*sin(2*pi/0.11*(x-1.00*t))only the resultant is visible to improve clarity of waveform.

Illustration of the envelope (the slowly varying red curve) of an amplitude-modulated wave. The fast varying blue curve is the carrier wave, which is being modulated.

Main article: Amplitude modulation

See also: Frequency modulation and Phase modulation

The amplitude of a wave may be constant (in which case the wave is a c.w. or continuous wave), or may be modulated so as to vary with time and/or position. The outline of the variation in amplitude is called the envelope of the wave. Mathematically, the modulated wave can be written in the form:^[10][11][12]

${\displaystyle u(x,t)=A(x,t)\sin(kx-\omega t+\phi )\ ,}$

where ${\displaystyle A(x,\ t)}$ is the amplitude envelope of the wave, ${\displaystyle k}$ is the wavenumber and ${\displaystyle \phi }$ is the phase. If the group velocity ${\displaystyle v_{g}}$ (see below) is wavelength-independent, this equation can be simplified as:^[13]

${\displaystyle u(x,t)=A(x-v_{g}\ t)\sin(kx-\omega t+\phi )\ ,}$

showing that the envelope moves with the group velocity and retains its shape. Otherwise, in cases where the group velocity varies with wavelength, the pulse shape changes in a manner often described using an envelope equation.^[13][14]

Phase velocity and group velocityEdit

Main articles: Phase velocity and Group velocity

See also: Envelope (waves) § Phase and group velocity

The red square moves with the phase velocity, while the green circles propagate with the group velocity

There are two velocities that are associated with waves, the phase velocity and the group velocity.

Phase velocity is the rate at which the phase of the wave propagates in space: any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and period T as

${\displaystyle v_{\mathrm {p} }={\frac {\lambda }{T}}.}$

A wave with the group and phase velocities going in different directions

Group velocity is a property of waves that have a defined envelope, measuring propagation through space (that is, phase velocity) of the overall shape of the waves' amplitudes – modulation or envelope of the wave.

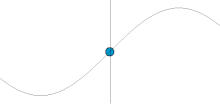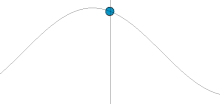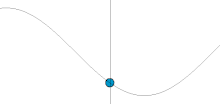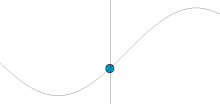
Sine wavesEdit

Main article: Sine wave

Learn more This section duplicates the scope of other sections, specifically, Sinusoidal wave and Frequency.

Sinusoidal waves correspond to simple harmonic motion.

Mathematically, the most basic wave is the (spatially) one-dimensional sine wave (also called harmonic wave or sinusoid) with an amplitude ${\displaystyle u}$ described by the equation:

${\displaystyle u(x,t)=A\sin(kx-\omega t+\phi )\ ,}$

where

• ${\displaystyle A}$ is the maximum amplitude of the wave, maximum distance from the highest point of the disturbance in the medium (the crest) to the equilibrium point during one wave cycle. In the illustration to the right, this is the maximum vertical distance between the baseline and the wave.
• ${\displaystyle x}$ is the space coordinate
• ${\displaystyle t}$ is the time coordinate
• ${\displaystyle k}$ is the wavenumber
• ${\displaystyle \omega }$ is the angular frequency
• ${\displaystyle \phi }$ is the phase constant.

The units of the amplitude depend on the type of wave. Transverse mechanical waves (for example, a wave on a string) have an amplitude expressed as a distance (for example, meters), longitudinal mechanical waves (for example, sound waves) use units of pressure (for example, pascals), and electromagnetic waves (a form of transverse vacuum wave) express the amplitude in terms of its electric field (for example, volts/meter).

The wavelength ${\displaystyle \lambda }$ is the distance between two sequential crests or troughs (or other equivalent points), generally is measured in meters. A wavenumber ${\displaystyle k}$, the spatial frequency of the wave in radians per unit distance (typically per meter), can be associated with the wavelength by the relation

${\displaystyle k={\frac {2\pi }{\lambda }}.\,}$

The period ${\displaystyle T}$ is the time for one complete cycle of an oscillation of a wave. The frequency ${\displaystyle f}$ is the number of periods per unit time (per second) and is typically measured in hertz denoted as Hz. These are related by:

${\displaystyle f={\frac {1}{T}}.\,}$

In other words, the frequency and period of a wave are reciprocals.

The angular frequency ${\displaystyle \omega }$ represents the frequency in radians per second. It is related to the frequency or period by

${\displaystyle \omega =2\pi f={\frac {2\pi }{T}}.\,}$

The wavelength ${\displaystyle \lambda }$ of a sinusoidal waveform traveling at constant speed ${\displaystyle v}$ is given by:^[15]

${\displaystyle \lambda ={\frac {v}{f}},}$

where ${\displaystyle v}$ is called the phase speed (magnitude of the phase velocity) of the wave and ${\displaystyle f}$ is the wave's frequency.

Wavelength can be a useful concept even if the wave is not periodic in space. For example, in an ocean wave approaching shore, the incoming wave undulates with a varying local wavelength that depends in part on the depth of the sea floor compared to the wave height. The analysis of the wave can be based upon comparison of the local wavelength with the local water depth.^[16]

Although arbitrary wave shapes will propagate unchanged in lossless linear time-invariant systems, in the presence of dispersion the sine wave is the unique shape that will propagate unchanged but for phase and amplitude, making it easy to analyze.^[17] Due to the Kramers–Kronig relations, a linear medium with dispersion also exhibits loss, so the sine wave propagating in a dispersive medium is attenuated in certain frequency ranges that depend upon the medium.^[18] The sine function is periodic, so the sine wave or sinusoid has a wavelength in space and a period in time.^[19][20]

The sinusoid is defined for all times and distances, whereas in physical situations we usually deal with waves that exist for a limited span in space and duration in time. An arbitrary wave shape can be decomposed into an infinite set of sinusoidal waves by the use of Fourier analysis. As a result, the simple case of a single sinusoidal wave can be applied to more general cases.^[21][22] In particular, many media are linear, or nearly so, so the calculation of arbitrary wave behavior can be found by adding up responses to individual sinusoidal waves using the superposition principle to find the solution for a general waveform.^[23] When a medium is nonlinear, then the response to complex waves cannot be determined from a sine-wave decomposition.

Plane waves

Standing waves

Physical properties

Mechanical waves

Electromagnetic waves

Quantum mechanical waves

Gravity waves

Gravitational waves

See also

References

Sources

External links

Last edited 2 days ago by Anita5192

RELATED ARTICLES

• Wavelength

  spatial period of the wave—the distance over which the wave's shape repeats, and thus the inverse of the spatial frequency
• Longitudinal wave

  waves in which the displacement of the medium is in the same direction as, or the opposite direction to, the direction of propagation of the wave
• Dispersion relation

  Relation of wavelength/wavenumber as a function of a wave's frequency

Content is available under CC BY-SA 3.0 unless otherwise noted.

• Terms of Use
• Privacy
• Desktop